参考资料
【算法】后宫三千如何友好相处?- N皇后排布问题 : 状态空间 与 状态迁移, 评估函数
前提假设

博弈树: 在当前局面下,后续n个回合行动后,所有的可能的局面。(结构如下图)
重要概念: min-max 搜索 与 局面评估。
默认具有良好的评估函数,将局面根据对自己的有利程度评分,越高越有利。
由于是回合制行动,一般评估双数步后的局面。在博弈树中,评估叶子节点表示的局面而不是非叶子节点。
min-max 搜索
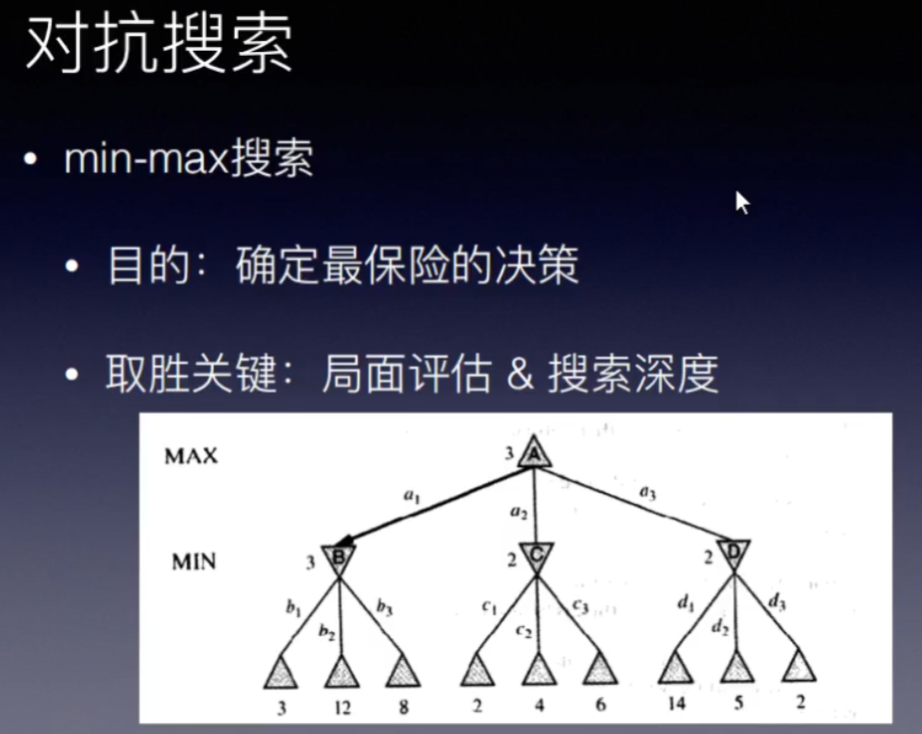
min-max 的含义: 将博弈树 以奇偶层数分为MAX层和MIN层。
MAX层的节点表示,这一层的所有节点(局面)可以由我方行动,可以选择最有利于我方的局面,局面评估分数尽可能高。
同理,MIN层节点,由对方行动,选择最有利于对方的局面,即最不利于我方的局面,局面评估分数尽可能低。
最后选择最保守的行动路线。
取胜的关键,就是局面评估和搜索深度。
局面评估函数越优秀,那么基于此函数的判断会更准确。
搜索得越深,看得步数越远,掌握的信息越多,越有可能获胜。看2步后和看8步后,显然是后者更可能获胜。
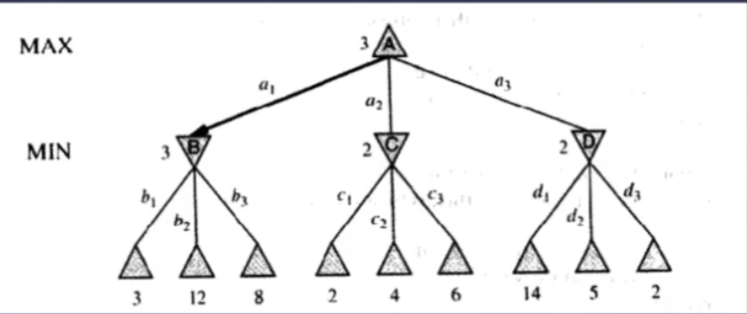
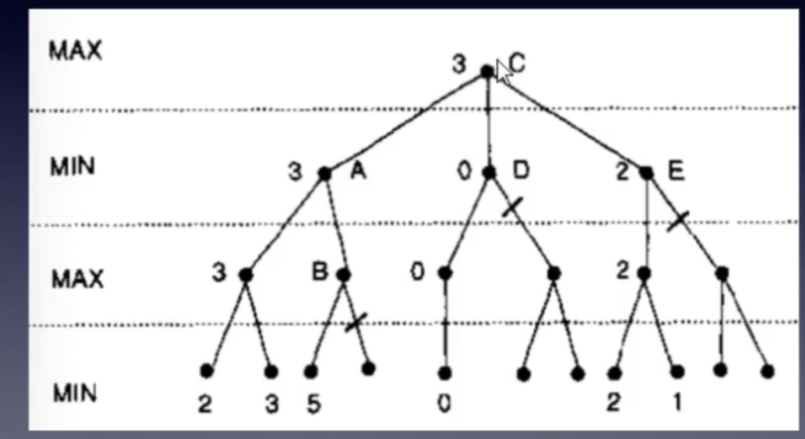
以上图为例,评估偶数步后叶子节点的局面得到分数。
MIN层(第二层),对方行动,要最不利我方,所以:
节点B选择 子节点中 分数最低的 3,走b1步。而不是走b2,给我方放水;
节点C 选择 分数 2 而不是6; 节点D选择2, 而不是14
MAX层(第一层), 我方心动,从节点BCD中选择最有利于我方的局面,分数3,走a1步。
如果看到更远,比如看到第四层,发现走a1步,会导致失败。走a2 局面分数会更高。也可是说明搜索深度越深,越有可能取胜。
αβ剪枝 - 优化方法
为了取胜,在同计算量下,怎样获得更深的搜索深度呢?采用αβ剪枝。
基本原理是:参考已经搜索到的分支的信息,减少不必要的搜索分支。
根据遍历顺序分为left-to-right和right-to-left两种,前者从左边开始遍历,后者从右边开始遍历,(差别不大不太重要)
一些学术化的表述,熟悉之后直接看这个:
对于每个max节点设置一个目前已知下界alpha,每个min节点设置一个目前已知上界beta。
但发生下面两种情况时可以剪枝,即停止搜索该节点的其余子节点:
1)当计算一个min结点时,如果它的beta值小于等于其父结点的alpha值,则可以立即停止此结点的计算(alpha剪枝)。
2)当计算一个max结点时,如果它的alpha结点大于等于其父结点的beta值,也可以立即停止此结点的计算(beta剪枝)。
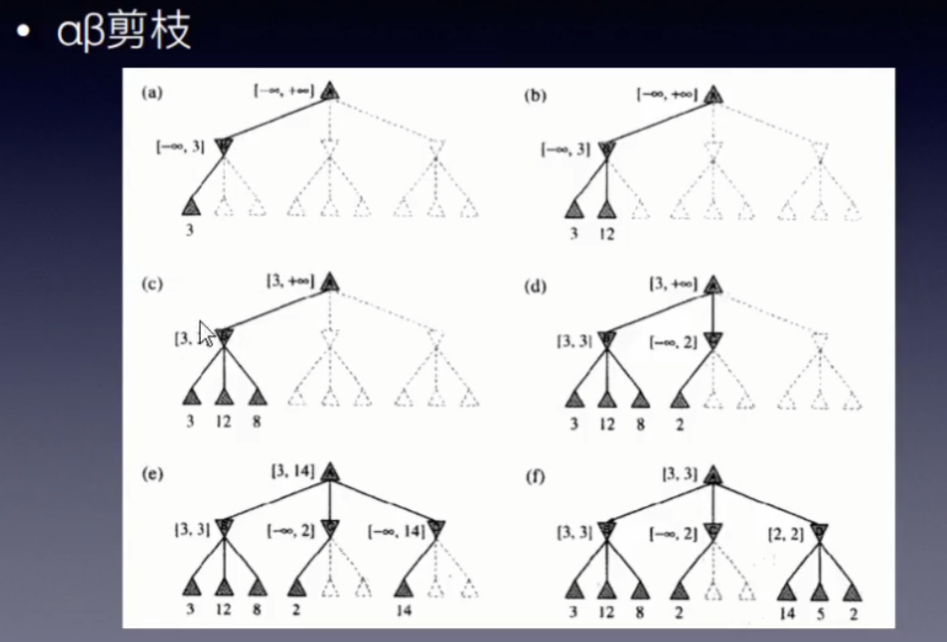
例子1,如上图。
过程(a),(b),(c) 和 普通的DFS是一样的,稍有不同的是信息更新。
过程(a)中,对于根节点(MAX层节点),先搜索最左边的分支,到节点B。对于节点B(MIN 层节点),搜索完最左边的分支后,得到分数3,则更新 β值为3,这是敌方能接受的最坏的局面,可接受的评估数值的上界。
过程(b), (c) ,将节点B下所有可能搜索完毕,可以确定MIN层节点B的值为 3,那么对于MAX层节点A,有了一个可选的值3,那么对于我方,更新α值,为3。表示,我方最差最差也有3分的局面可选,不会选择更差的局面了,即可接受的下界。
进入过程(d),也是先DFS,发现了一个可选的局面2,MIN层节点C,更新β值为2,。此时需要考虑一下了。对于当前局面(根节点),已经有分值3的局面可选了,节点C 最高也只有2,那么可以剪除剩余的分支,不搜索。
进入过程(e), 剪除了节点C 的剩余分支后,节点C搜索完毕,进入节点D搜索,依旧是普通的DFS。发现14,更新节点D的β值为14,大于节点A的α值3,节点A的可以达到的局面分数范围为[3,14],接着在节点D下搜索。
过程(f),完成节点D的所有局面搜索,过程中,不断更新节点D的β值,直到最后一种可能的局面搜索完才发现节点D 的 β值小于 根节点A的 α值,那么 对于当前局面根节点A,在两步之后的最优局面 分数评估为 3。
例子中解释了剪枝规则1) 计算min节点时的判断。
对于剪枝规则2),计算max节点时,
如例子还有没有展示的更深层节点,对于过程(b)中,节点B下评分为12的子节点,
如果 其α值更新为12之后,发现自己的α值大于父节点的β值,
那么敌方肯定不会选择走到节点,放弃该节点下剩余其他可能的搜索是合理的。
例子2:
根据剪枝规则,例子2的剪枝是很容易理解的。先DFS,最左侧的叶子结点都搜完之后,评估所有已知局面,往上更新上层节点的α和β值。之后接着DFS,使用αβ剪枝。
局面评估
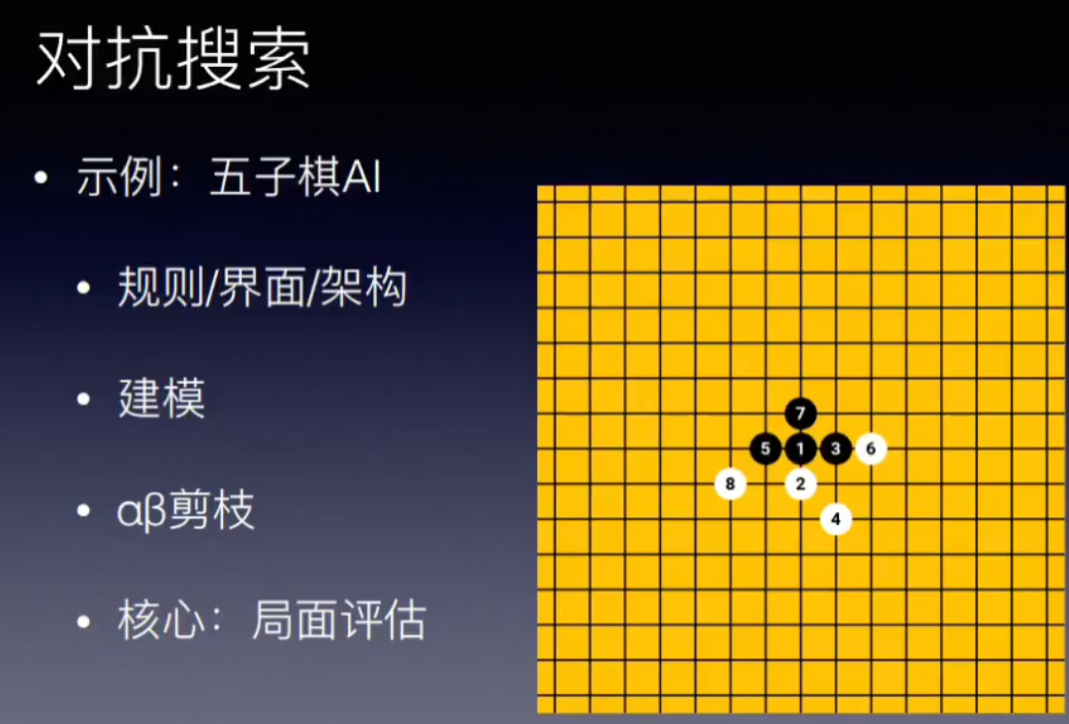
局面评估是棋类AI的核心,min-max搜索和αβ剪枝 是 搜索框架 两者结合才是一个合格的AI

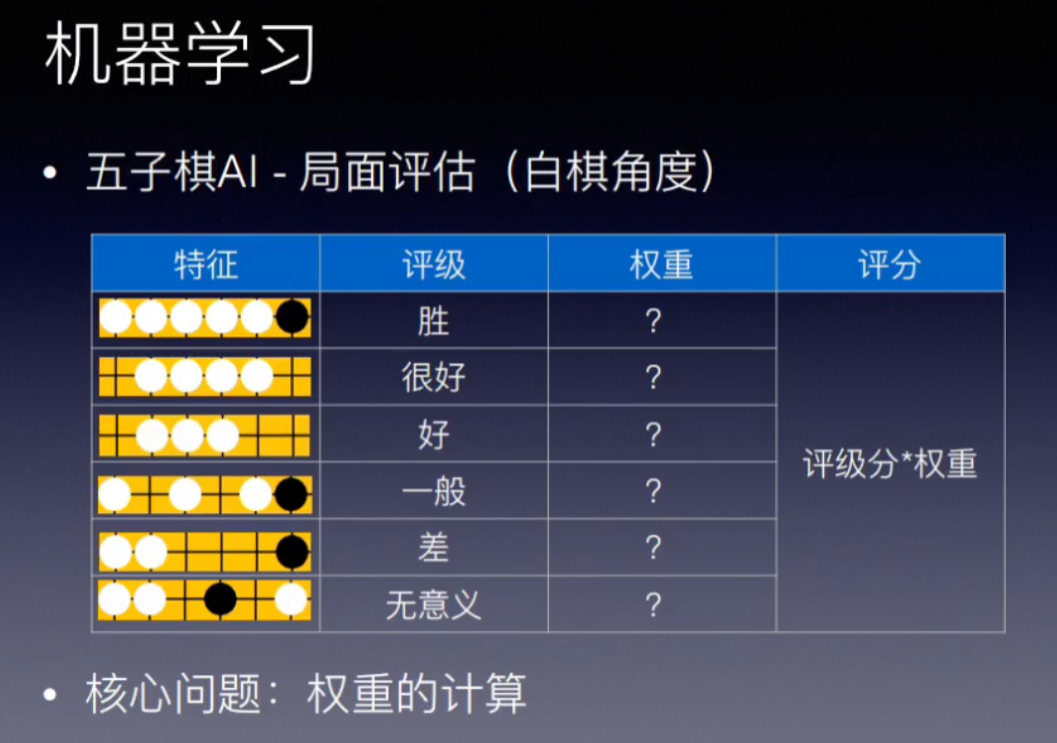
建模:采用的特征是,一定长度直线的棋子排布。最后对于所有个特征进行一个线性相加。
一个棋类AI的功能是 给一个局面,返回一个下一步趋向获胜的行为。
有了博弈树和min-max搜索(αβ剪枝)将这个问题转化为-局面评估问题。
通过建模,将局面评估转化为 权重的计算问题。
权重其实就是一组向量,有一定的取值范围,定义了一个状态空间。其中每个状态有好有差。 这个与N皇后问题,启发式算法(爬山算法,退火算法)有关。
可以使用练蛊的方法(随机获得多组值,两两PK循环赛,取前几名,再随机获得多组值,再PK)
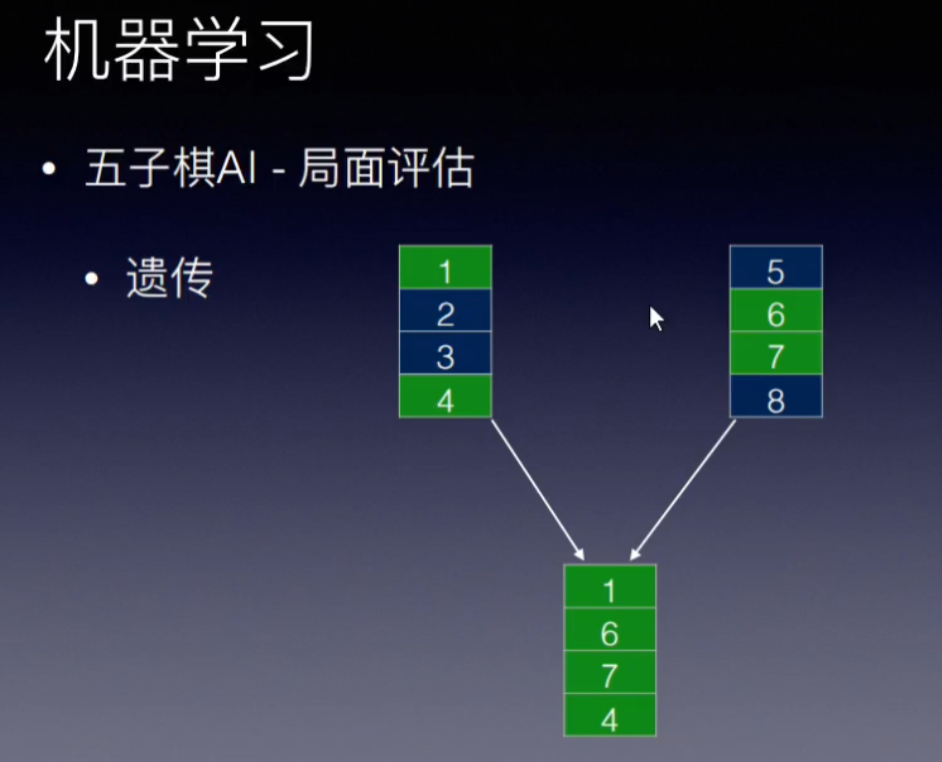
也可以使用遗传算法,通过遗传(集中已有的优势基因)和变异(突破当前所有存在基因的上限) ,获得比较强势的一组值。
局限性,1. 建模并没有充分考虑多条线之间的影响。
2. 搜索深度不足。
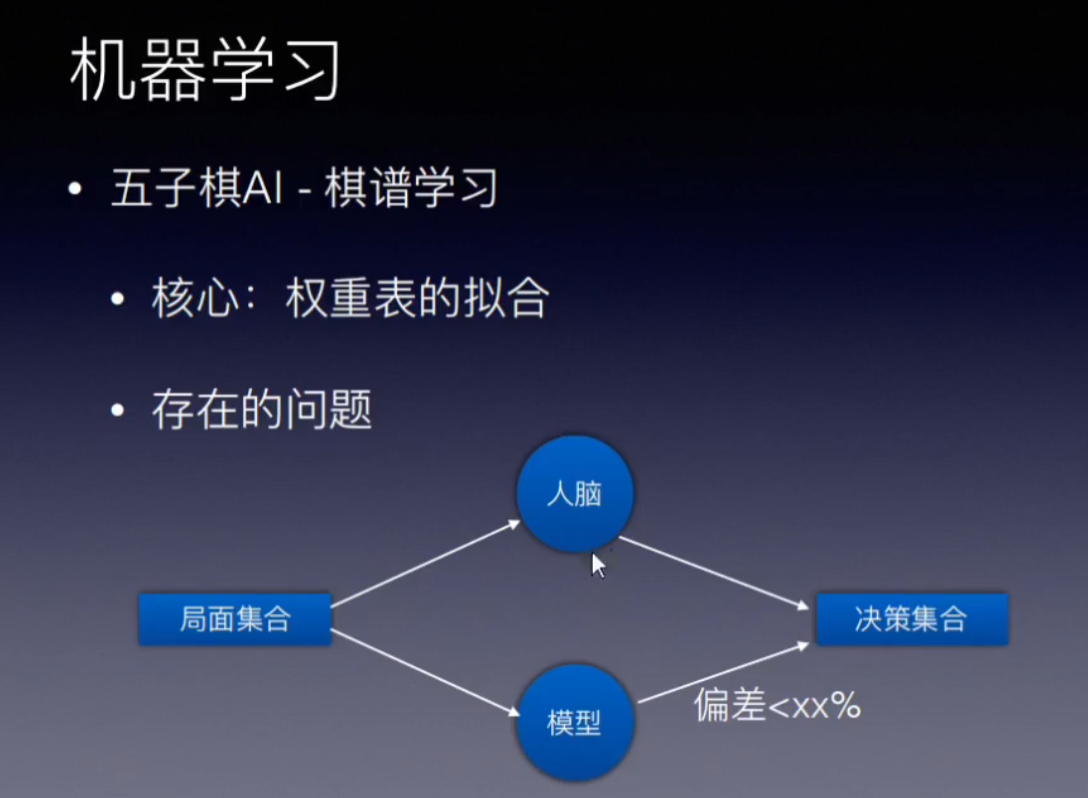
棋谱学习: 权重表的拟合,给棋谱,调整权重表,是的下一步的结果符合棋谱的设定。当误差率低到一定程度,那么这个AI就接近人脑。